

2021年05月23日
遺伝的アルゴリズムとは効率的な最適解を検索するアルゴリズムです。

これをシステムトレードのバックテストに適用して利益の出る手法を効率よく探索するために使います。
遺伝的アルゴリズムへの適用のために、システムトレードの手法をどのようにして遺伝子の形に落とし込むか説明します。
インディケータの遺伝子表現では以下のことが表現できるようにします。
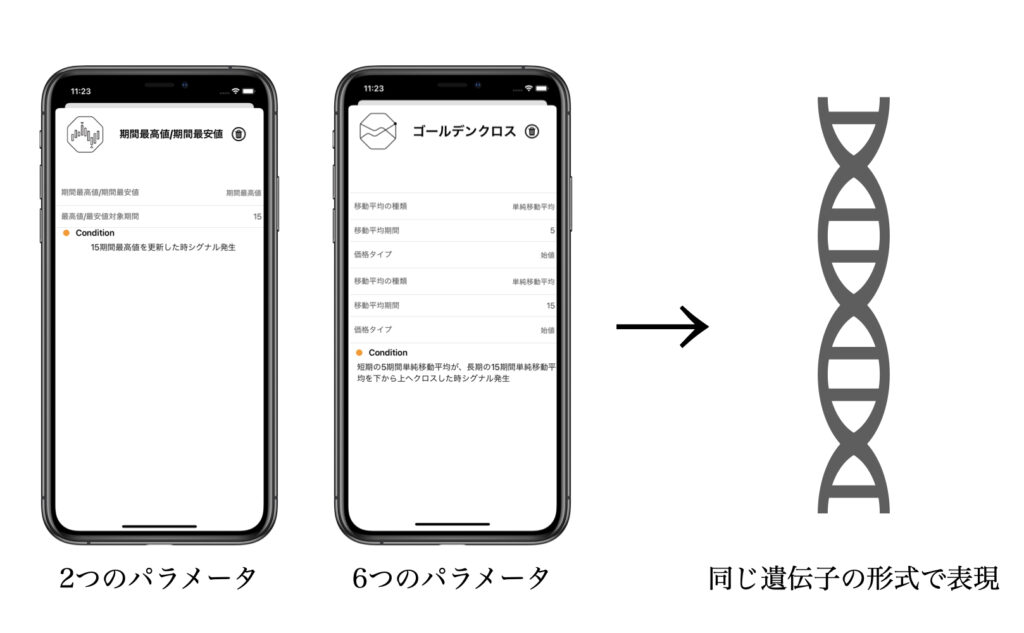
『どのインディケータも同じ形式で表現できるようにする』
パラメータが2つの期間最高値/期間最安値もパラメータが6つのゴールデンクロスも同じ遺伝子型で表せるようにします。
遺伝的アルゴリズムの遺伝子型は実数型とビット型に分かれます。
システムトレードでのパラメータはボリンジャーバンド2.6σといった具合に実数を取ることもあります。
しかし、移動平均期間は整数で少数を含まなかったり、
移動平均の種類『単純移動平均』『加重移動平均』『指数平滑移動平均』『可変指数動的平均』のように選択肢型のパラメータがあります。
そのため、ビット型の遺伝子で表現することにしました。
ビット表現は一つ一つの要素を0,1で表現します。
その0,1がいくつか連なり2進数として数値を表します。
例えば、4bitの0111は8×0+4×1+2×1+1×1=7となります。
一般的な2進数で表現する場合、問題があります。それは隣り合う数字が大きく異なる点です。
例えば、上の2進数で7から8になると 0111→1000 と4つ全てのbitが変化します。
もし、最適解が8で現状の遺伝子が7の場合、8へ行くには4つの変化が必要となり、遺伝的アルゴリズムの性能が大きく悪化します。
逆に2進数で0100→1100と変化した場合、1bitの変化しかありませんが、4→12と大きく変化してしまいます。
遺伝的アルゴリズムでは親から子へ似た遺伝子を受け渡していくアルゴリズムです。その際、多少の変化で大きく値が変わってしまうのは好ましくありません。
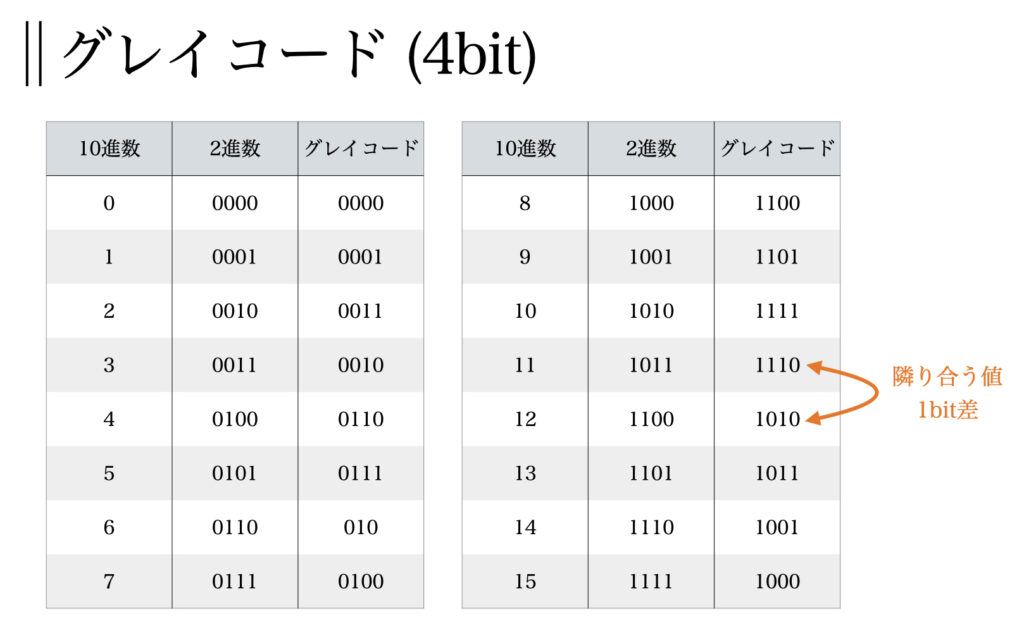
そこでグレイコードを使用します。これにより上記の問題を解決できます。
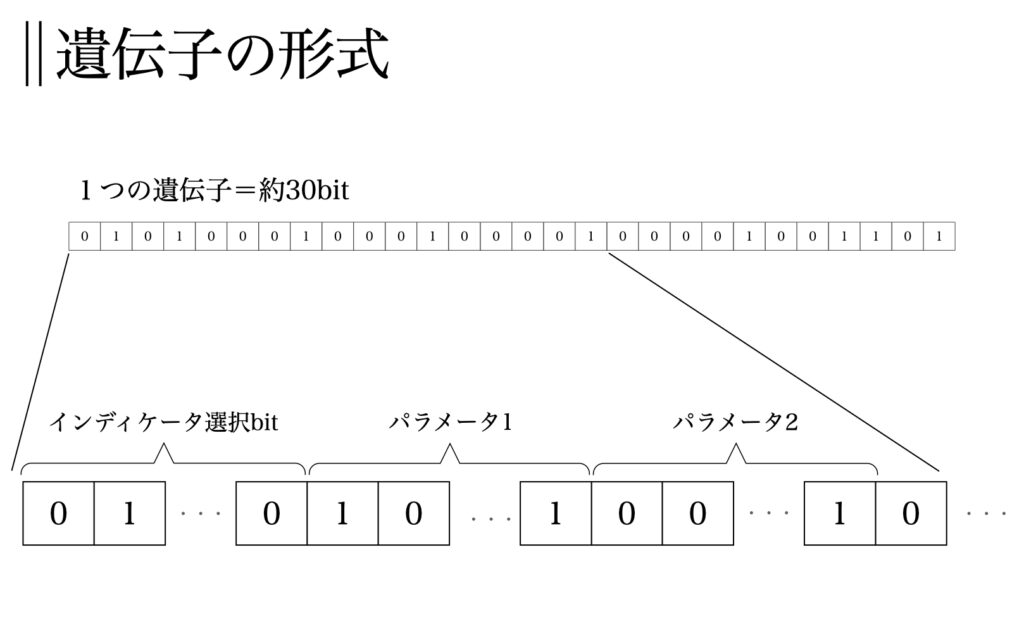
遺伝子の頭の数bitをインディケータ選択部分、残りをパラメータ部分とします。
パラメータは前述の通りインディケータによって数が異なりますので、bitを長めに設定し、少ないパラメータのインディケータは後ろの部分が不要になります。
インディケータ選択方法はインディケータ選択bitのグレイコードでの数値に応じて決定し、下のような形で選択されます。
といった具合です。
パラメータもグレイコードの値を元に表現されます。しかし、パラメータによっては整数の値だけを取るものや、少数も取るもの、マイナスの値を取るものから、0から100のものまで
範囲も取る値も様々です。
そこで各パラメータに範囲と刻みを決めます。
例) 移動平均期間の場合 整数 1~128と設定
7bitの長さが割り当てられる
グレイコードによる値Gは0~127を取る
移動平均期間=G+1
例) ボリンジャーバンドのσの場合 実数 -3.2~3.2で0.1刻み
6bitの長さが割り当てられる
グレイコードによる値Gは0~63を取るので、スケール係数を0.1として
σ=G×0.1-3.2
このように刻みと範囲に応じてbitの長さを決め、スケール係数をかけ、範囲内となるよう足し引きします
これにより、遺伝子⇄インディケータの変換ができるようになりました。
一般的なバックテストでの遺伝的アルゴリズムは特定のインディケータの特定のパラメータを変数としたものが多いです。
つまり、ゴールデンクロスの移動平均を変数(=遺伝子)として、どの移動平均が最適なのか探索するものでした。
一方今回の実装であれば、特定のインディケータに固定しないで遺伝的アルゴリズムを適用することができます。
どのインディケータ同士を組み合わせてシステムトレード戦略とするのが良いかという
より自由度の高い探索ができるようになりました。
コントラは最高のFXアプリを
目指して誠意開発を続けております。
機能の要望や、不具合などありましたらご遠慮なくヘッダーの問い合わせ、フィードバックからご連絡ください。またツイッターからでも大丈夫です!
皆様のFXトレードのお力になるFXアプリを目指しますので、これからもよろしくお願いいたします。