

2021年03月13日
ここではADALINE学んでいく。
前回のパーセプトロンでは学習方法について取り扱わなった。その理由はADALINEの学習方法と比較しながら学んで欲しかったからである。
最適化の登場はとても重要です。
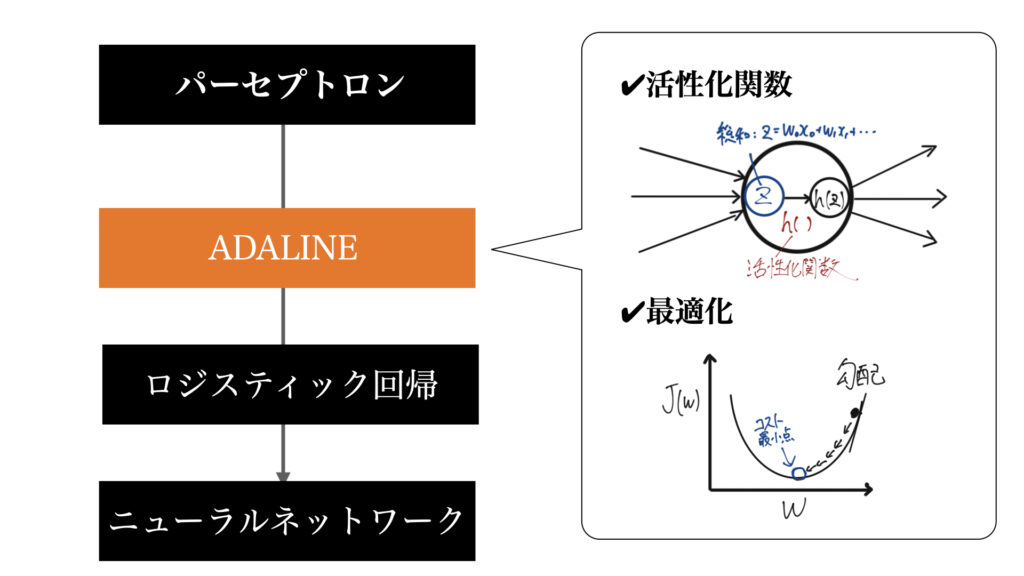
ADALINE=ADAptive LInear NEuron
読み方はアダリン
直訳すると適応線形ニューロン
パーセプトロンと比べれば活性化関数が増えただけのニューロンである。パーセプトロンアルゴリズムから数年後に発表されたもので、改良版パーセプトロンといったところ。
こちらはパーセプトロン
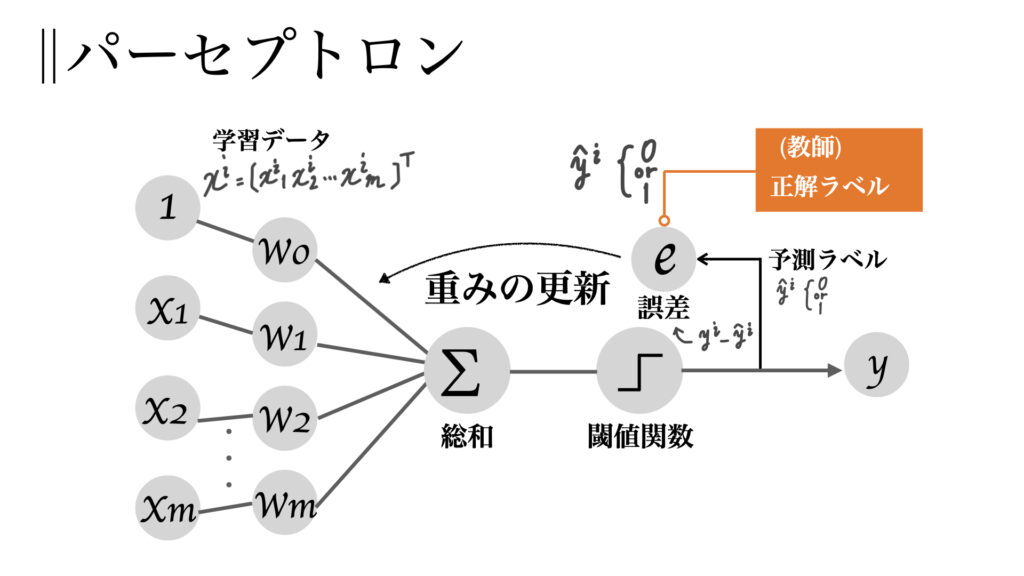
そしてこちらがADALINE
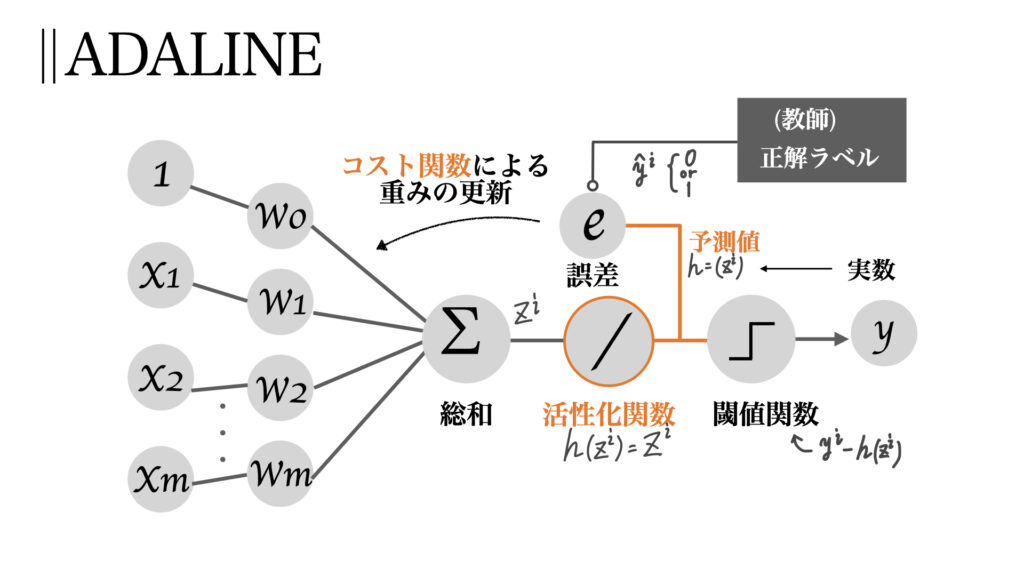
ということでパーセプトロンの学習について理解した後、その違いを交えてADALINEアルゴリズムを理解していただきたい。
なお、前回の復習ではあるが学習とは重みの自動設計である。
ではまずパーセプトロンにおける学習法について見ていこう。
アルゴリズムとしてはとても単純で以下のように書ける。
初期重みは0か0に近い小さい値を用いる。
出力値はパーセプトロンの記事で説明した通り0 or 1である。
重みの更新は以下の様に更新される。
$$w_j:=w_j+\Delta w_j=w_j+\eta(y^i-\hat{y}^i)x_j^i$$
$$\Delta w_j=\eta(y^i-\hat{y}^i)x_j^i$$
ここで\(\eta\)は学習率というもので、一回の学習でどのくらい値を更新するかを決定するパラメータである。0から1の間で設定する。

\(y^i-\hat{y}^i\)は正解と予測の差、つまり予測誤差であり、パーセプトロンでは信号は0 or 1であるので正解していたら0つまり更新なし、間違っていたら\(\eta x_j\)だけ更新ということになる。
全ての重みが更新された後、次の学習データで同様の手順を踏む。
ではこのアルゴリズムの単純な例を見てみよう。
\(x_j^i\)が0.4で正解ラベルが1の時、このサンプルを誤って0と分類した。すると、
$$\eta=0.5,~\delta w_j=\eta(y^i-\hat{y}^i)x_j^i=0.5(1-0)0.4=0.2$$
となり、
$$w_j:=w_j+0.2$$
と重みが大きくなる。
重みが大きくなるということはその信号が閾値を超えて1と分類されそうになることが分かるだろう。
このように重みを更新していき、最終的に全ての学習データで正しく分類できた時にアルゴリズムは終了する。これを収束と呼ぶ。
しかし、いかなる時でも収束するとは限らない。
収束するための条件は、
である。
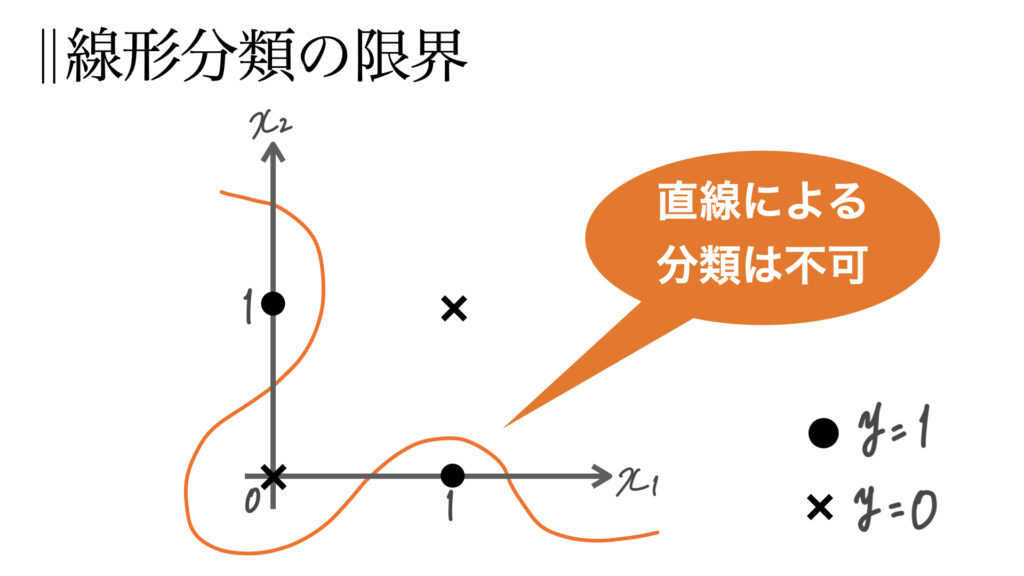
1つ目の条件は(単層)パーセプトロンでは線形分類しかできないことを学んだのでアルゴリズムが収束しないことが分かるだろう。
2つ目の学習率に関しては、学習率が大きいと1回あたりの重みの更新幅が大きくなる。するといつまで経っても適切な値にたどり着かないことがある。
小さすぎたらそれはそれで問題である。
なぜならたどり着くまでの回数が増大し収束まで時間がかかりすぎてしまうからだ。

この収束性と速度はトレードオフの関係であること、
そしてこれはニューラルネットワーク、ひいては最適化全般においても同様であることを覚えておいてほしい。
パーセプトロンでは分類が正しいか間違っているかで学習をしていた。でもこれでは効率が悪い。
そこで活性化関数を導入し、コスト関数を用いた最適化の概念を導入した。
それがADALINEである。
それでは本題であるADALINEでの学習に移る。ADALINEはパーセプトロンに活性化関数を加えたものである。
この活性化関数の導入によって重みの更新方法が進化した。
パーセプトロンでは答え合わせをクラス分けの⚪︎か×かで重みの更新を行なっていた。
一方、ADALINEでは活性化関数によって得られた連続値に対して答え合わせをする。
間違っている時は間違っているにしてもどの程度間違っているかを見て学習を行おう!
まず活性化関数とは何か。活性化関数とは入力信号の総和を出力信号に変換するもの
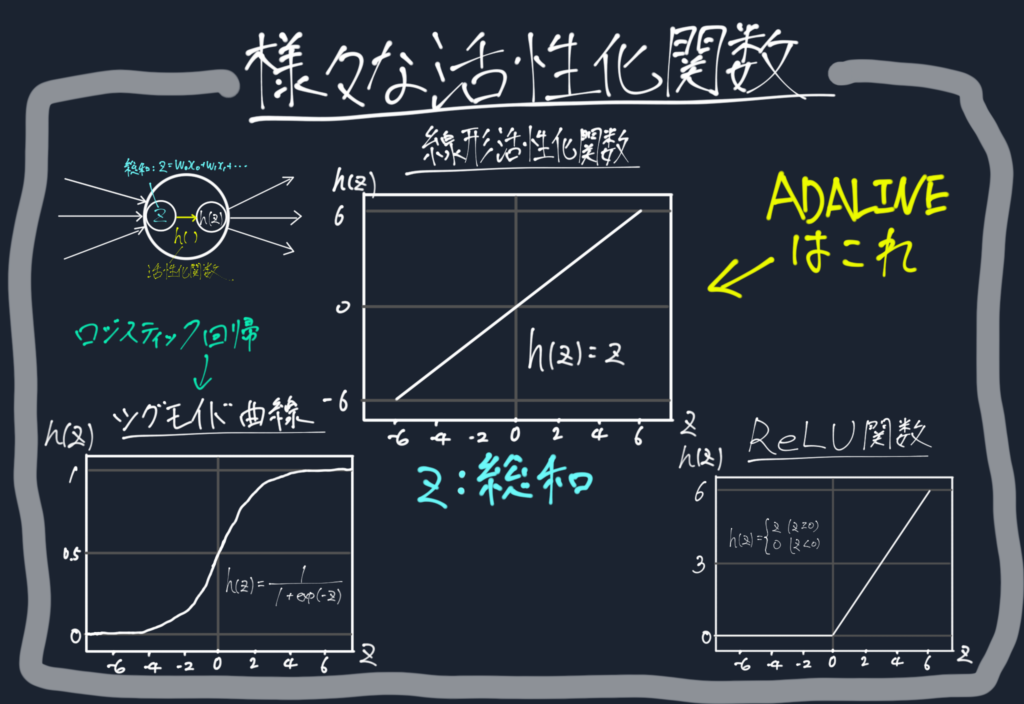
活性化とあるように活性化関数は入力信号の総和をどのように活性化(=ニューロンの発火)させるかを決める関数である。
この活性化関数は様々な種類がある。
ADALINEでは線形活性化関数、恒等関数ともいう
$$h(z)=z$$
が用いられる。
実質なくても同じになっている。しかし、微分可能という点で最適化においてこの活性化関数の恩恵を受けるのだ。
活性化関数を置くことで目的関数というものを定義できるようになった。目的関数とは最適化を行う際に、何が最適なのかを定めるもの
最適な学習をしよう!と決めたところで、
そもそも何が最適なのかを決めないと最適化できないよねという話。
そこでまず最適化の目的である目的関数を決める。
一般的に目的関数は最小化をしたいコスト関数が用いられることが多い。
コスト関数はコストという名の通り減らしたいものであり、ADALINEでは予測誤差をコスト関数として定義する。
$$J(w)=\frac{1}{2}\sum_{i}(y^i-h(z^i))^2$$
これは誤差平方和(Sum of Squared Error)といい、実際のクラスと予測値の差の2乗を全ての学習データに関して足し合わせたものである。
パーセプトロンのように個々のデータで評価し更新するのではない。データセット全体で評価し更新する。ここも大きな違い。
そしてなにより連続値の線形活性化関数を用いた最大の利点、それは、線形活性化関数の利点
なぜ微分可能になると嬉しいのか、それは容易に最適化を行うことができるから。勾配降下法を使って。
原理はコストが最小ないし極小値に達するまで減少する方へ下っていくアルゴリズム。
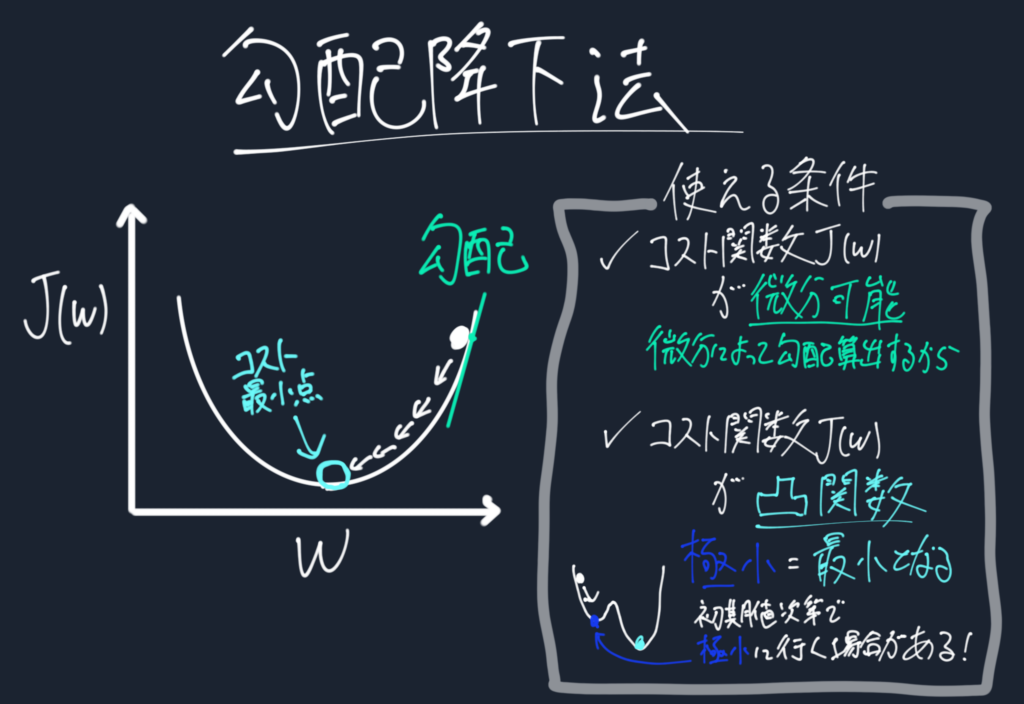
コスト関数の勾配\(\Delta J(w)\)の逆向きに少しずつ移動していけば、いずれ勾配が0、つまり最小値までwが移動していくことがわかる。なので更新方法は、
$$w=w+\Delta w=w+(-\eta\Delta J(w))$$
として、勾配は
$$\frac{\delta J}{\delta w_j}=-\sum_i(y^i-h(z^i))x_j^i$$
と求められるので、
重みwの更新は
$$\Delta w_j=-\eta\frac{\delta J}{\delta w_j}=\eta\sum_i(y^i-h(z^i))x_j^i$$
となる。
以上まとめるとADALINEの学習アルゴリズムは以下のようになる。
本記事ではADALINEを理解するためにパーセプトロンの学習方法と比較し、説明した。
ここで登場した最適化とそれに関わる目的関数・コスト関数はニューラルネットワークでも用いられる重要な内容である。
これらを理解したら、次はロジスティック回帰である。ニューラルネットワークはもうすぐそこ。

コントラは最高のFXアプリを
目指して誠意開発を続けております。
機能の要望や、不具合などありましたらご遠慮なくヘッダーの問い合わせ、フィードバックからご連絡ください。またツイッターからでも大丈夫です!
皆様のFXトレードのお力になるFXアプリを目指しますので、これからもよろしくお願いいたします。