

2021年02月26日
ここではパーセプトロンについて説明していく。
ニューラルネットワークの歴史で学んだように、パーセプトロンはニューラルネットワークの元祖ともいわれるモデルであり、とても簡単なモデルである。
しかし、ニューラルネットワークの基本的な概念である入力・出力・重みを持ち、またバイアスや多層化という考え方もパーセプトロンによって学ぶことができる。
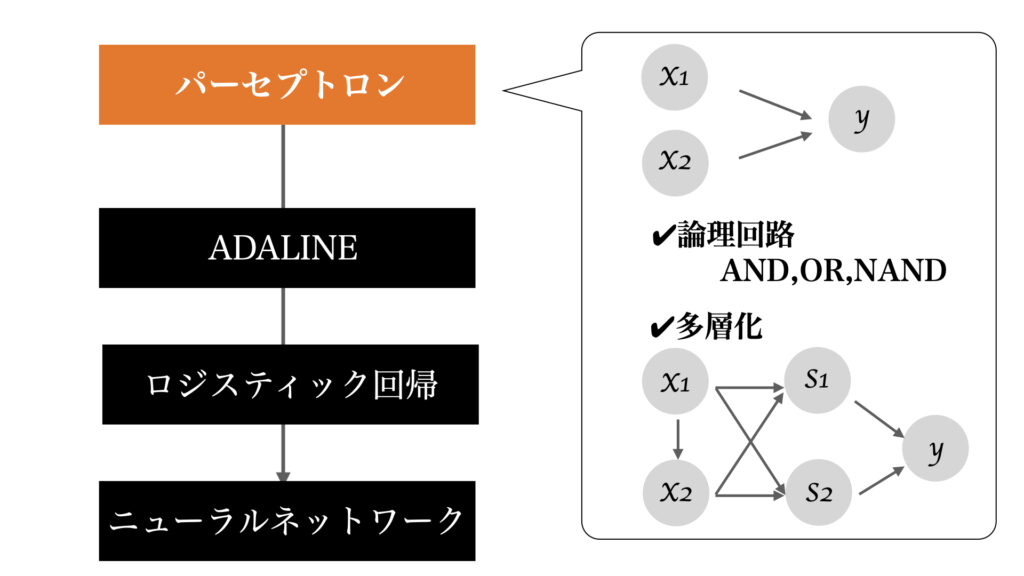
パーセプトロン複数の入力信号を受け取り、1つの出力信号を出すもの
そしてこのパーセプトロンにおける信号とは
流す or 流さない → 1 or 0
である。とてもシンプル。
以下の図が2入力の場合のパーセプトロンである。
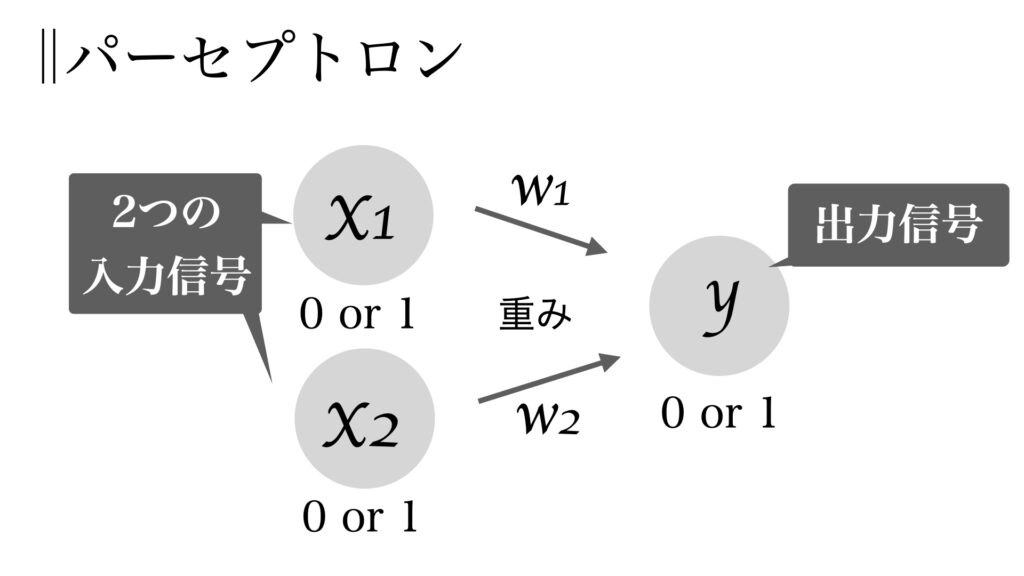
入力と出力と重みそして閾値\(\theta\)を用いて以下の計算が行われる。
$$ y=0~(w_1x_1+w_2x_2\le \theta)$$
$$ y=1~(w_1x_1+w_2x_2>\theta)$$
計算もとてもシンプル。式の意味は閾値を超えたら
\( y = 1 \)として信号を流す、これをニューロンの発火ともいう。
超えなかったら\( y = 0 \)で流さない。
しかしこの形式はニューラルネットワークにおいても用いられ大変重要である。
そしてこの重み\(w\)とやらがと最も重要な値なのである。
なぜなら、
パーセプトロンもニューラルネットワークも全て
この重みを丁度良い重みにすることを目指すからだ。
学習とは丁度良い重みを見つけること!
そして丁度良い重みを(自動で)探し方こそがニューラルネットワークというアルゴリズムである。
ここでひとまず今後のために
表現と式をバイアスを用いて変形する。
パーセプトロンの構成要素は入力、出力、重み、そして閾値であった。
この閾値も重みの中に組み込んでしまおう、ただ普通の重みとは役割が違うので名称だけバイアスにしようと言うのがこの話。
まず先程の式\( w_1x_1+w_2x_2\le \theta \)において、\( b=-\theta \)とする。
$$ b+w_1x_1+w_2x_2\le 0 $$
と書き換えることができる。つまり、
$$ y=0~(b+w_1x_1+w_2x_2\le0)$$
$$ y=1~(b+w_1x_1+w_2x_2>0)$$
と書ける。
バイアス\(b\)も名称は違えど通常の重みとして表現したい。\(w_0=b,~x_0=1\)とすれば,
$$ b+w_1x_1+w_2x_2=w_0x_0+w_1x_1+w_2x_2 $$
と書ける。
2入力の場合を見てきたが、3以上の入力でも良いのでこれを多入力として一般化する。
$$ y=0~(w_0x_0+w_1x_1+\cdots+w_mx_m =\sum_{j=0}^m x_jw_j \le 0$$
$$ y=1(w_0x_0+w_1x_1+\cdots+w_mx_m =\sum_{j=0}^m x_jw_j > 0$$
このようにして多入力パーセプトロンを表現できた。図示すると以下の様になる。
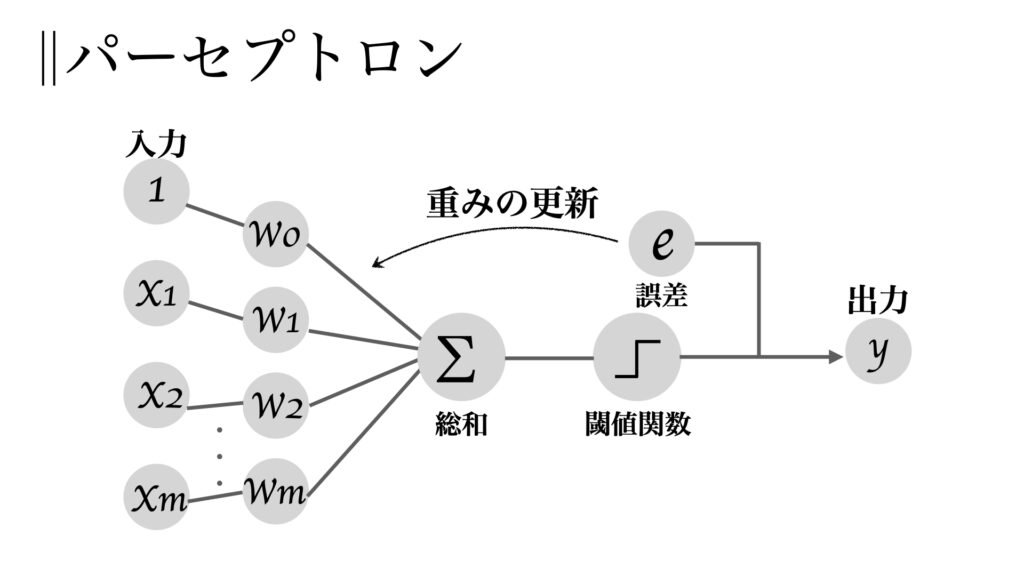
重みの学習に移りたいところだが、その前にパーセプトロンで出来ることを説明しよう.
なにができるのだろうか?

パーセプトロンが出来ること、それは論理演算(ANDとかOR)である。
パーセプトロンの流すことができる信号が1 or 0 (=true or false)であることからもお気付きだったかもしれない。
ではまずANDゲートを表現してみよう。
ANDでは以下の処理を行う。
| $$x_1$$ | $$x_2$$ | $$y$$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
これをパーセプトロンで表現する、言い換えればANDの処理を行う重みの決定である。
決定すべき重みは
$$ (w1, w2, /theta=-b) $$
の3つ。選び方は無限にあるが、例えば
(w1, w2, /theta) =(0.3, 0.4, 0.5), (1, 1, 1)
などが考えられる。ANDゲートが出来た。
次はOR。
| $$x_1$$ | $$x_2$$ | $$y$$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
(w1, w2, /theta) =(0.6, 0.7, 0.5), (1, 1, 0.9)
などで表現できる。
NANDではx1x2の両方が1の時のみ0を返す。
| $$x_1$$ | $$x_2$$ | $$y$$ |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
これはマイナスの重みを使えば良い。
(W1, w2, /theta) =(-0.4, -0.5, -0.6), (-1, -1, -1.1)
のようにして表現できる。
このようにパーセプトロンによってAND、OR、NANDが表現できることを確認した。
では次にXOR(排他的論理和)を表現してみる。
しかし、これまでのように簡単にはいかない。
XORは以下のような処理である。自分以外は認めない(排他的)感のある処理だ。
| $$x_1$$ | $$x_2$$ | $$y$$ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
これをグラフに図示してみる。
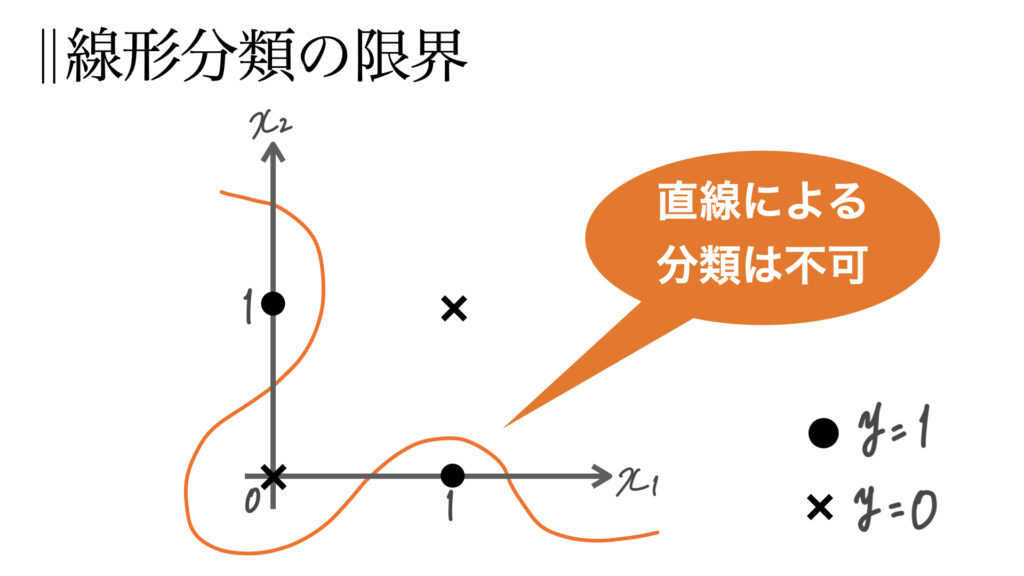
パーセプトロンには限界があった。それは線形(直線)分類しかできないのである。(x1w1+x2w2の式からも線形しか表現できないことが分かる)
上図をうまく分類するには非線形の関数を用いなくてはならない。
ではどうするか?
ここで多層化が登場する。
パーセプトロンは層を重ねることができる。
これは重要な特性であり、ニューラルネットワークへ引き継がれていく。
そしてこれによって(単層では)表現できなかったXORも表現できるようになる。
ではまず、XORゲートを今まで作成したAND, OR, NANDで表現してみる。
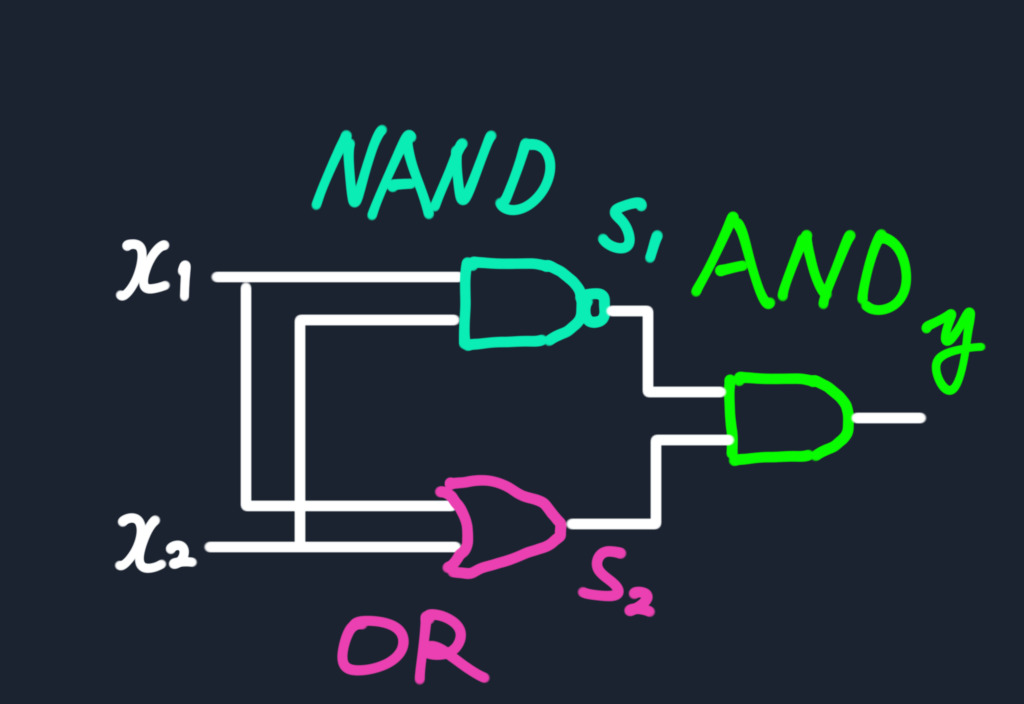
NAND, OR, ANDの組み合わせでXORがこのように表現できる。
となると、先ほど作ったパーセプトロンを3つ組み合わせれば以下の様にしてXORを作ることができるのだ。
これは三層構造にも見えるが、重みと出力処理を行っているのは2層であるため、これは2層パーセプトロンと呼ばれる。
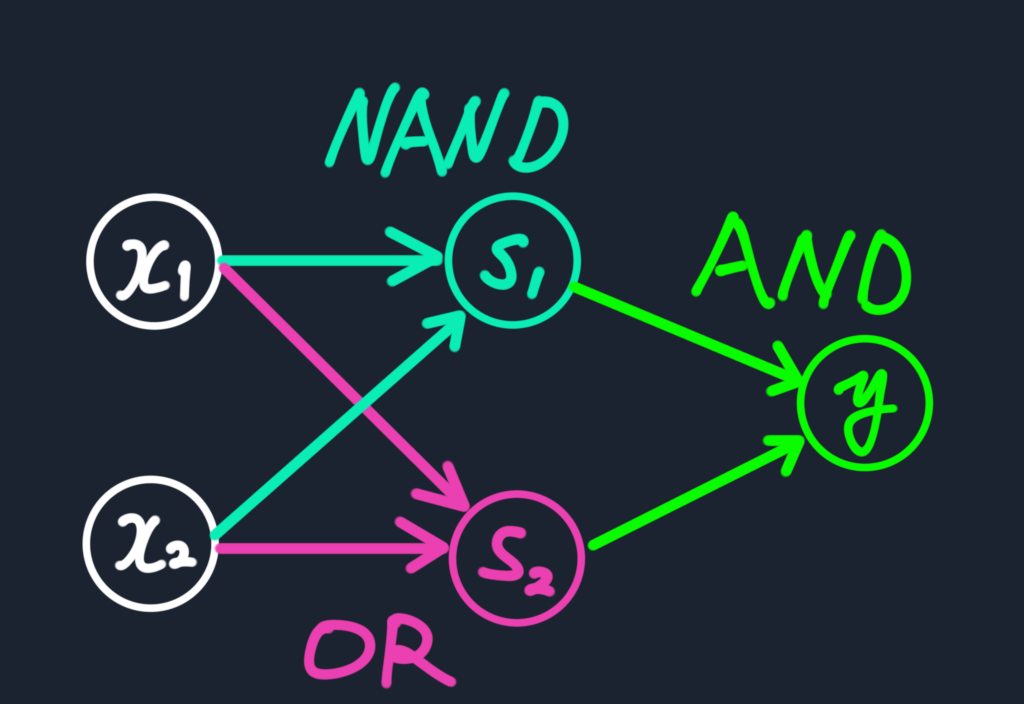
これは三層構造にも見えるが、重みと出力処理を行っているのは2層であるため、これは2層パーセプトロンと呼ばれる。
このようにパーセプトロンの多層化によって単層では表現できなかったものを表現できるようになった。
そして論理演算子NANDは全ての論理演算を表現できる、という性質がある。
これはつまり、NANDを作れるパーセプトロンは(多層化を用いることで)全ての論理演算を表現できるということ。

ということは計算機、さらにはコンピュータもこの1 or 0の論理演算処理を行うパーセプトロンで表現することができるのだ!
ここではニューラルネットワークの元祖であるパーセプトロンを扱った。
非常に簡単な論理演算処理しか出来ないが、多層化という重要な概念を用いることで複雑な表現も可能になることがわかった。この多層化はニューラルネットワークにおいても非常に重要である。
ニューラルへの道は、最適化による学習という概念が加わったADALINEへと続いていく。

コントラは最高のFXアプリを
目指して誠意開発を続けております。
機能の要望や、不具合などありましたらご遠慮なくヘッダーの問い合わせ、フィードバックからご連絡ください。またツイッターからでも大丈夫です!
皆様のFXトレードのお力になるFXアプリを目指しますので、これからもよろしくお願いいたします。