

2021年03月11日
システムトレード基本と原則 7-8章
トレーディングという授業があるとしたら、この3単元からなると言っても過言ではありません。
そして、1番重要なのが資金管理です。

少しでも期待値がプラスの売買ルールさえあれば、この資金管理さえしっかりできれば、破産もせず資産を伸ばしていくことができます。
心理状態が悪くても、資金管理できていれば、破産しません。
だから1番重要なのです。
資金管理の答えはこれです。
トレーディングで損失が出たらポジションを減らし、利益が出たらポジションを増やすのだ。
システムトレード基本と原則 8章
正解はこれしかなく、あとはハイリスクハイリターンかローリスクローリターンどちらを選ぶかという問題です。
資金管理の目的、なんのために資金管理をするか明確にしておきましょう。
つまり、守りと攻めのための資金管理です。

守り、つまり生き残る→破産確率を下げる話はこちら
ただ一般に、生き残る(=破産しない)と大きな利益を得ることは、互いにトレードオフの関係
つまり、大きな利益を得るにはリスクが必要だし、生き残るのを重視すれば慎重になり利益は小さくなってしまいます。
そこでどうするか。それは先人達(トレードの成功者)を真似しましょう。
この考え方は逆マーチンゲール法と呼ばれる資金管理方法です。
マーチンゲール法はその逆で、負けた時はその次は勝ちやすいと考え、
倍掛けして損失を取り戻すという理屈に従った方法です。
これは、とても危険な考えで、破産確率が急上昇します。
資金が少ない時により多くのリスクを取ると、賭ける資金の割合が急増するし、負けた後に勝つ保証なんて全くないためです。

このような方法はギャンブラーに任せておいて、我々は逆マーチンゲール法、つまり
負けたら減らし、勝ったら増やす
を徹底しましょう。
先に具体的な資金管理方法を記述しておきます。
逆マーチンゲール法で最もポピュラーな方法です。
取引量 = (定率 ✖︎ 口座残高) ÷ 1トレードでのリスク
例えば口座残高が¥3,000,000で、5%までのリスクを許容
使っているトレード戦略での1取引量(1Lotや単元株)でのリスクが¥50,000の場合
3Lot(単元株数、枚)での取引となります。
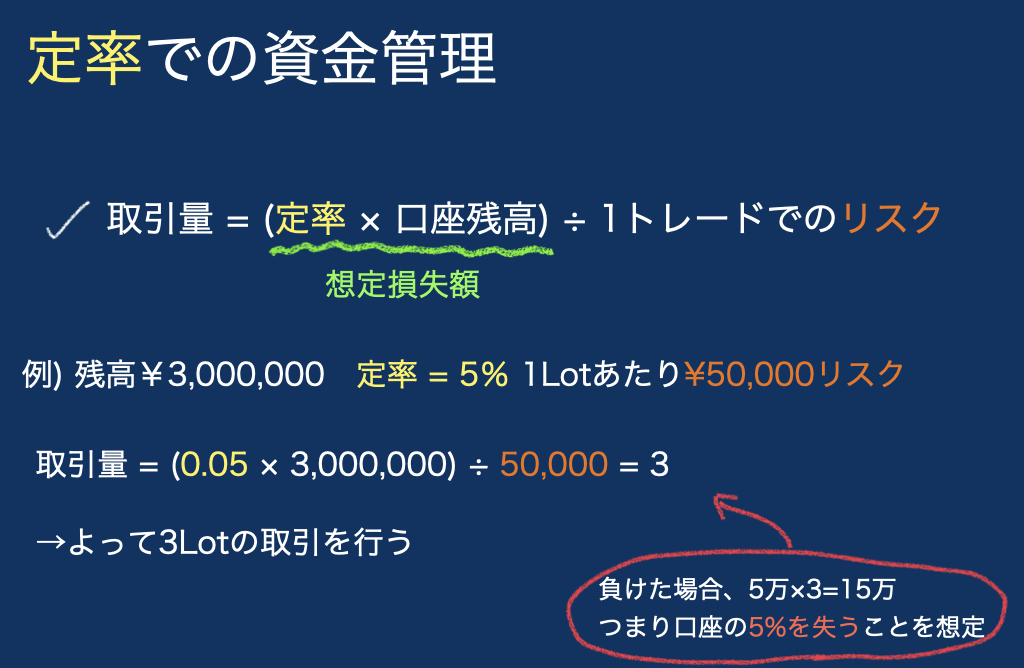
口座残高が¥4,000,000になれば4Lotになり、逆に負けて¥2,000,000になると2Lotとなります。
しっかり逆マーチンゲール法に従っていることがわかります。
資産をN%失うとどういうことが起こるかというと『非対称なレバレッジ』が発生します。
Q. 30%の資産を失ったとすると、それを取り戻すのにどれだけ利益を出せばいいか?
70%を100%に持っていく必要があるため、100/70 ≒ 143%
つまり、43%の利益を出さないといけません。
一度資産を失うと、元手が減少してしまうため、
それだけ取り戻すのに、少ない元手で取り返す必要があります。
例のように70%の資産で100%まで戻すには30%ではなく、43%の利益が必要となるのです。
失う時と取り戻す時に必要な利益が非対称であるため、非対称なレバレッジというわけです。
ドローダウンのダメージはここにあり、少ないドローダウン(10%)であれば復帰も早い(11%利益で良い)ですが、
大きなドローダウン(50%)の場合、復帰が相当厳しく時間もかかります(100%利益が必要)。
| 損失 | 必要な利益 |
| 10% | 11% |
| 20% | 25% |
| 30% | 43% |
| 40% | 67% |
| 50% | 100% |
なので、ドローダウンをできるだけ小さくしたいと望み、戦略を考えるべきなのです。
逆マーチンゲール法では特に、負けた時は賭ける量を減らすため損失を取り戻すのに時間がかかります。
もちろん逆マーチンゲール法であろうとなかろうと必ずこの非対称なレバレッジで苦しむことにはなります。
この点も資金管理では考慮する必要があり、いくつかの方法が考えられています。
今回は逆マーチンゲール法という資金管理の基本原則と、1番ポピュラーな定率による方法を紹介しましたが、
他にもいくつか紹介すべき方法があります。
次の記事をお待ちいただければと思います。
手法をまとめた続編の記事がこちらです。

そしてそれらを数値シミュレーションによって検証した続々編はこちらです。

コントラは最高のFXアプリを
目指して誠意開発を続けております。
機能の要望や、不具合などありましたらご遠慮なくヘッダーの問い合わせ、フィードバックからご連絡ください。またツイッターからでも大丈夫です!
皆様のFXトレードのお力になるFXアプリを目指しますので、これからもよろしくお願いいたします。